DFS, BFS [파이썬]

DFS, 깊이 우선 탐색

간단 개념

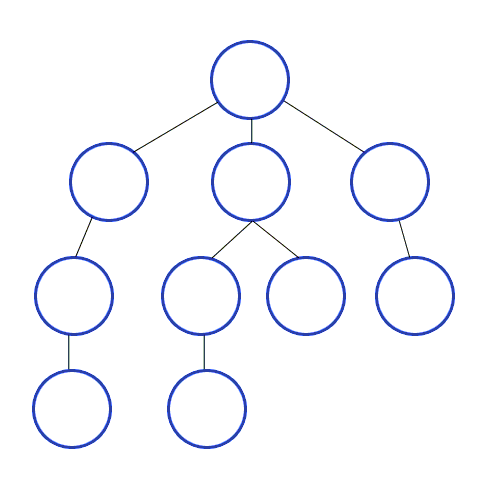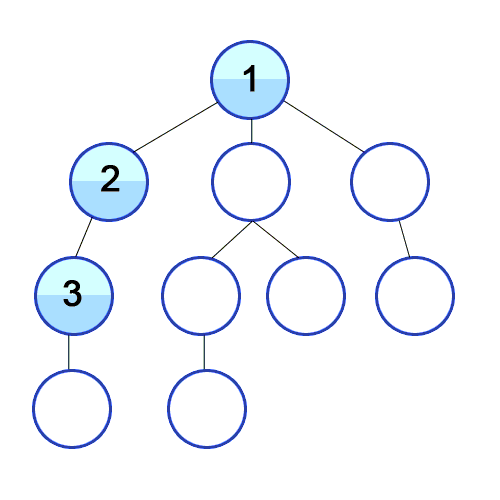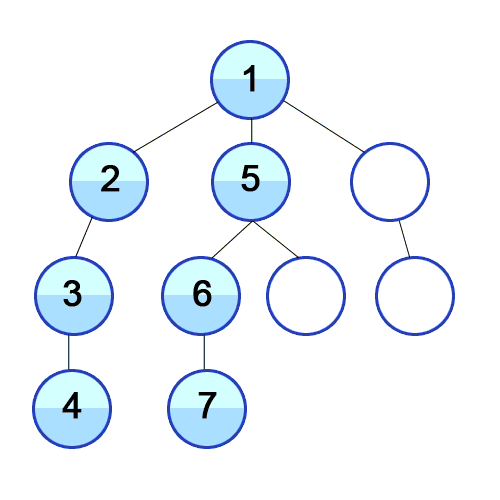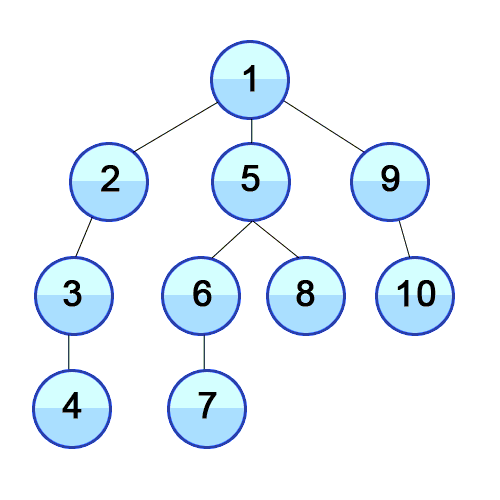출처 https://developer-mac.tistory.com/64

트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙히 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식. 재귀호출, 스택 두가지 방법이 모두 가능하다.

구현하기 - 스택

1. 스택을 하나 만든다. 빈 스택에 시작할 노드를 넣는다.
2. 스택에서 노드를 하나 꺼내고(pop), 출력한다. 그리고 꺼낸 노드의 자식 노드들을 다 넣는다.
   (❗이때 한 번 스택에 담은 노드는 다시 넣지 않음)
3. 반복한다.

이때 기억해야 할 점은 스택이기 때문에 마지막으로 넣은 노드부터 탐색된다.

구현하기 - 재귀

일반적으로 코드가 깔끔하기 때문에 선호하는 방법이다. 노드에 방문하면 그 노드를 출력하고 그것의 자식들을 재귀 호출한다.

1. 노드의 자식의 자식의 자식..을 계속 호출하고 들어간 다음
2. 더이상 자식이 없으면 하나 올라와서 올라온 지점의 다른 경로로부터 탐색을 다시 시작한다.

       1
    /  |  \
   2   3   4
   |   |
   5   |
  / \ /
 6   7

이런 그래프가 있으면 재귀 호출은

dfs(1)
    dfs(2)
        dfs(5)
            dfs(6)
    dfs(3)
            dfs(7)
    dfs(4)

이렇게 된다.

📃 소스코드

"""
       1
    /  |  \
   2   3   4
   |   |
   5   |
  / \ /
 6   7
"""

graph = {
    1: [2,3,4],
    2: [5],
    3: [5],
    4: [],
    5: [6,7],
    6: [],
    7: [3],
}

def recursive_dfs(v, visited = []):
    visited.append(v) # 시작 정점 방문
    for w in graph[v]:
        if not w in visited: # 방문 하지 않았으면
            visited = recursive_dfs(w, visited)
    return visited

def iterative_dfs(start_v):
    visited = []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in visited:
            visited.append(v)
            for w in graph[v]:
                stack.append(w)
    return visited

print("recursive_dfs: ", recursive_dfs(1))
print("iterative_dfs: ", iterative_dfs(1))

# 스택은 마지막에 스택에 담은 정점부터 꺼내져 방문되기 때문에
# 재귀 방식과 결과가 다름.

BFS , 너비 우선 탐색

간단 개념

출처 https://developer-mac.tistory.com/64

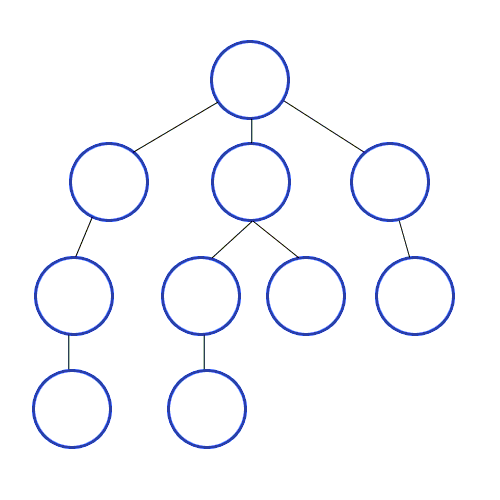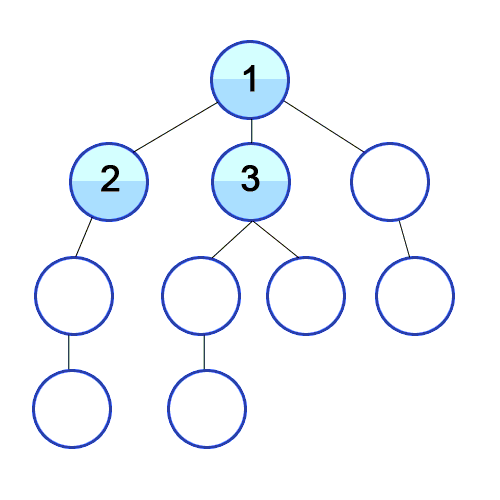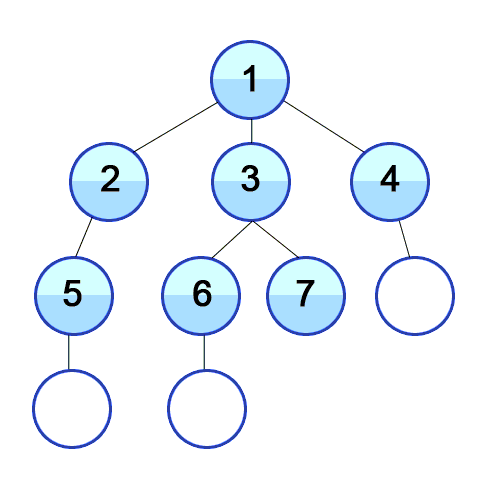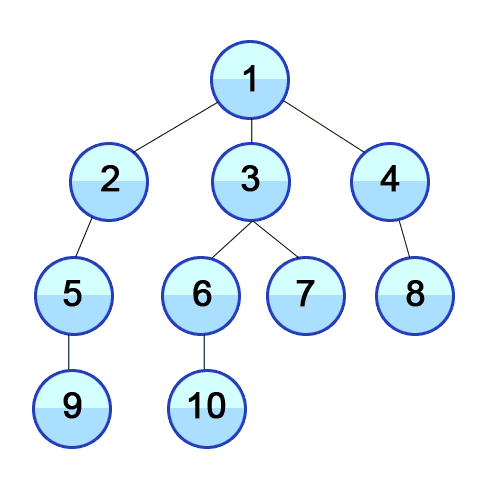
시작 노드로부터 가까운 지점을 먼저 방문하고 먼 지점은 나중에 방문한다.

• 무한한 길이를 가지는 경로가 존재할 때 탐색 목표가 다른 경로에 있을 경우
  • DFS는 영원히 종료하지 못하지만
  • BFS는 모든 경로를 거의 동시에 진행하기 때문에 탐색이 가능하다 큐로 구현이 가능하며 재귀는 불가능하다.

구현하기 - 큐

큐는 선입 선출(FIFO) 이다.

1. 빈 큐를 만들고 시작 노드를 넣는다.
2. 큐에서 노드를 꺼내고(pop), 출력한다. 꺼낸 노드의 자식들을 큐에 추가한다
   (❗이때 한 번 큐에 담은 노드는 다시 넣지 않음)
3. 반복한다.

📃 소스코드

"""
       1
    /  |  \
   2   3   4
   |   |
   5   |
  / \ /
 6   7
"""

from collections import deque

graph = {
    1: [2,3,4],
    2: [5],
    3: [5],
    4: [],
    5: [6,7],
    6: [],
    7: [3],
}

def bfs(start_v):
    visited = [start_v]
    deq = deque()
    deq.append(start_v)
    while deq:
        v = deq.popleft()
        for w in graph[v]:
            if w not in visited:
                visited.append(w)
                deq.append(w)
    return visited

print("bfs: ", bfs(1))

"""
bfs:  [1, 2, 3, 4, 5, 6, 7]
"""

출처

너무 설명을 간단 명료하게 하셔서 그대로 참조했습니다.